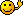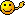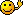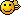Also, wenn man mal die beiden großen Klammern auflöst und die Brüche multipliziert, erhält man:ich habe auch eine frage.
ich sitz nun schon seit 2 stunden an dieser rechnung:

herauskommen sollte x². ich krieg aber immer 1 heraus, egal was ich mache!!
könnte mir jemand den rechenweg erklären // vorrechnen?
Danke Schonmal!
x^(2*2) * y^4 . x^4 * y^4
------------- = ---------
y^(2*2) * x^4 . y^4 * x^4
Und hier kürzen sich die ganzen x und y weg, weil oben jeweils 4 sind und unten auch. Macht:
1
- = 1
1
So wie es da steht kommt tatsächlich 1 raus, da sich alles wegkürzt.
@laloup:
1.) Fläche Rechteck: 7,7cm*4,4cm = 33,88cm²
Quadrat mit 33,88cm² hat als Seitenlänge Wurzel(33,88cm²) = 5,82cm.
2.) und 3.) sieht richtig aus.
@littlebear:
Wenn mit der 1. Achse die x-Achse gemeint ist, dann ist eine Parallele davon einfach eine konstante Funktion g(x) = c.
Diese schneidet f(x) im Punkt (z, z²) = (z, c). D.h. c=z² und somit, z = Wurzel(c).
F(x) = 1/3 * x³, G(x) = c*x, die Fläche zwischen den beiden geht von 0 bis z und berechnet sich als
Integral(c*x - 1/3 * x² dx, x=0..z) = 8/3 * Wurzel(2)
und somit nach Einsetzen
c*z - 1/3 * z³ = 8/3 * Wurzel(2).
Ich hab einfach die Differnez der beiden Funktionen genommen und integriert um die Fläche dazwischen beschreiben zu können.
Stellt man den ganzen Quatsch um erhält man für c den Wert DritteWurzel(32) = 3,1748 und so den Schnittpunkt mit z = SechsteWurzel(32).
Setzt man das in der Probe ein, erhält man 2/3*Wurzel(32) = 2/3*4*Wurzel(2) = 8/3*Wurzel(2).
Das alles aber auch nur, wenn die 1.Achse wirklich die x-Achse ist. Hab den Begriff 1. Achse noch nie gehört.
Für alles gilt: Alle Angaben ohne Gewähr.